Investigating Internal Representations of Correctness in SONAR Text Autoencoders

TL;DR: We probed SONAR text autoencoders to see if they implicitly learn "correctness" across domains. Turns out they do, but with a clear hierarchy: code validity (96% accuracy) > grammaticality (93%

---

ARENA Context

This research was completed during the final week of ARENA 5.0 bootcamp. Despite some technical hiccups, we each invested roughly 4 days into this project. Goals: a) showcase our work, b) highlight ARENA's value, and c) make a genuine (if small) contribution to mechanistic interpretability. Anton and I did a small-scale MechInterp project on the internal embeddings of SONAR, a text autoencoder by Meta, following up some initial work by NickyP. Anton focused on the language manifold in SONAR, while I focused on investigating the degree to which SONAR encodes correctness. Anton’s contribution can be found here (link following soon).

Abstract

We investigated whether SONAR text autoencoders develop internal representations of "correctness" across multiple domains: language grammaticality, mathematical validity, code functionality, and chess legality/semantics. SONAR text autoencoders function by encoding text into a fixed-size sentence embedding using a Transformer-based encoder and then reconstructing the original text from this embedding with a corresponding decoder. Using PCA visualization and logistic regression probes, we found a clear hierarchy of correctness understanding, with strongest signals in code validity and language grammaticality, yet no signal for more complex reasoning domains.

Introduction and Motivation

Research Question: Do text autoencoders implicitly learn concepts of "correctness" to aid reconstruction?

Hypothesis: Since autoencoders compress sequences into sentence embeddings for reconstruction, maintaining correctness information should facilitate better decoding. If you're trying to reconstruct something from a compressed representation, knowing it follows certain rules makes the job easier.

Domains Tested:

• Grammaticality (across languages)

• Mathematical correctness (arithmetic)

• Code validity (Python functions)

• Chess legality and semantics

Our approach was admittedly limited. We used the same two hammers (PCA + logistic regression) for every nail we encountered. But sometimes simple tools reveal interesting patterns.

Why is this relevant for AI Safety? SONAR isn't a scary model, but that's exactly why it's useful. It's a transformer-based model organism that lets you do mechanistic interpretability work without melting your GPU or your budget. More importantly, understanding "agent overhang", how much reasoning capability is lurking in models, is crucial for estimating risks in larger systems.

Moravec's paradox applies here: a language model's learning curriculum doesn't mirror human development. What seems "easy" to us might be hard for the model, and vice versa. The hierarchy we found (code > grammar > arithmetic > chess) doesn't follow intuitive difficulty rankings. This matters because if we can't predict capability emergence in simple models, we're flying blind with larger ones.

Even "stupid" models can surprise you. Understanding their exact capabilities isn't just academic. It's practice for the harder problem of interpreting systems that actually matter for safety.

The compression efficiency explanation also has implications: if correctness emerges from compression rather than explicit training, then capability might be more predictable from architectural and data choices than we think. Or it might be less predictable if compression dynamics are chaotic. Either way, we need to find out on models we can actually understand.

Methodology

Model: SONAR text autoencoder

I will refrain from explaining the SONAR model’s architecture; there is already a great write-up on this on LessWrong. We utilized the same “hammer” for all of the following experiments:

1. Extract sentence embeddings for correct/incorrect examples

2. Visualize with PCA for linear separability

3. Train logistic regression probes for classification

4. Test cross-domain generalization

The core idea: if the model stores correctness information, we should be able to extract it from the internal representations, and use it to linearly predict correctness from the embeddings.

Results

Grammaticality: The Foundation

Initial Experiment: Fed random sentences vs grammatical sentences into the model, then applied PCA. Clear separation emerged, but this wasn't representative. Random text isn't the same as ungrammatical text.

Refined Experiment: Created pairs of grammatical and ungrammatical sentences, where the latter were generated by jumbling word order of the former. This controlled for vocabulary and content while isolating grammaticality.

Figure 1: 2D PCA representation of individual sentence embeddings. Each dot represents a sentence embedding, where red is from grammatical English sentences, and blue is from agrammatical English sentences.

Figure 2: Distribution of Direction Scores for grammatical vs. agrammatical sentences. Scores are derived by projecting SONAR sentence embeddings onto the weight vector of a trained logistic regression probe. The separation of the grammatical (green) and agrammatical (red) distributions confirms that the probe successfully identified a linear direction for grammaticality within the model's embedding space.

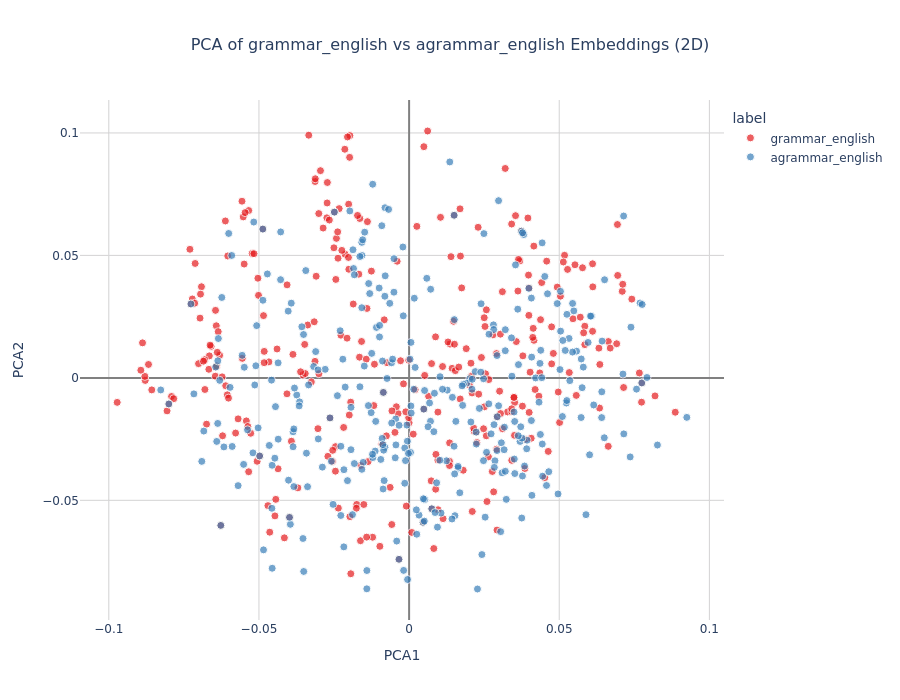
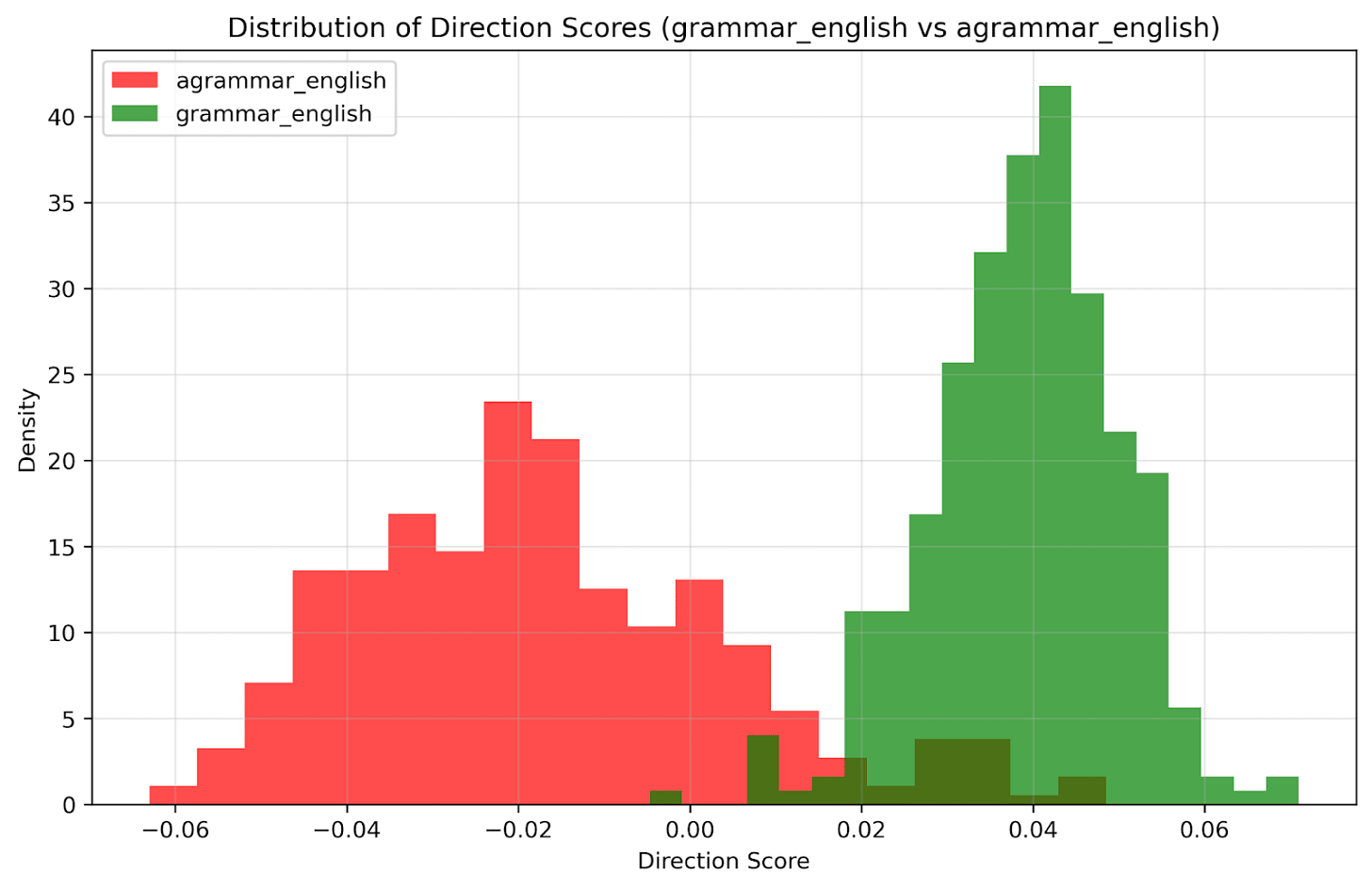
Results:

• No clear linear separation with PCA alone

• Logistic regression achieved 94% train, 93% test accuracy

• Crucially: The same grammaticality direction, extracted from the logistic regressor weights, held across languages

• Weights from English grammaticality probes successfully classified grammaticality in other languages

Interpretation: The model develops language-agnostic grammaticality representations, suggesting it captures universal syntactic patterns rather than language-specific rules.

Mathematical Correctness: Limited Scope

Next up, we investigated how far this “grammaticality”-understanding goes. We asked ourselves: How much does the model actually "reason" about its encodings? Does it go beyond surface-level language patterns to something resembling logic?

Experiment Setup: Trained logistic regressors on sentences like "The result of X + Y is Z" where Z was either correct (X + Y) or incorrect (random number).

Figure 3: 2D PCA representation of individual sentence embeddings for math experiment. Each dot represents a sentence embedding, where red is from correct math sequences (i.e. "X + Y is Z" is actually correct), and blue is from incorrect math sequences.

Figure 4: Distribution of Direction Scores for correct vs. incorrect math sequences. Scores are derived by projecting SONAR sentence embeddings onto the weight vector of a trained logistic regression probe. The separation of the incorrect (green) and correct (red) distributions confirms that the probe successfully identified a linear direction for correct math sequences within the model's embedding space. Notice the bimodal nature of the correct math sequences – some sequences were identified wrongly as incorrect.

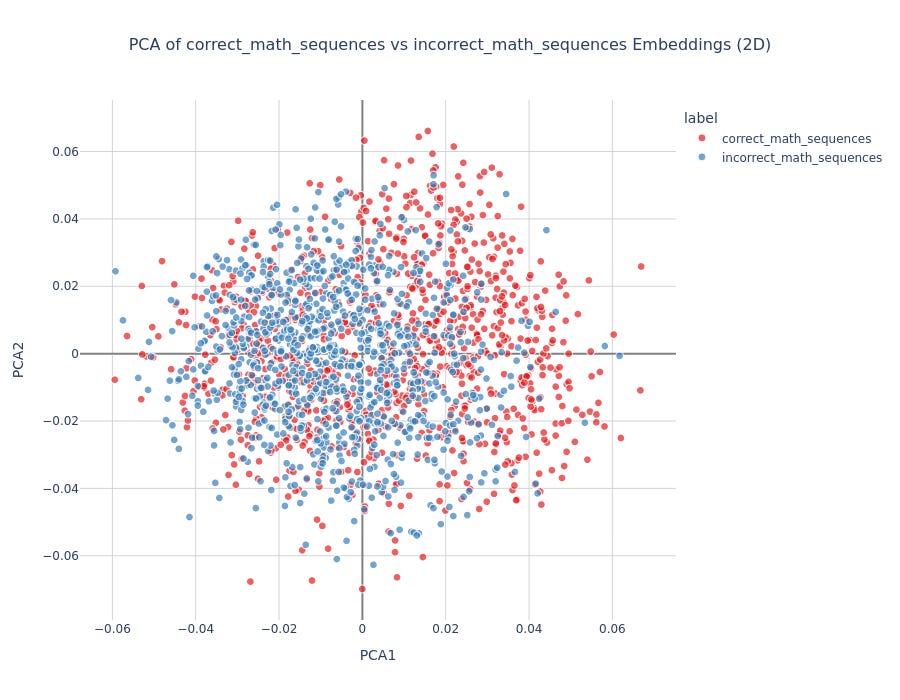
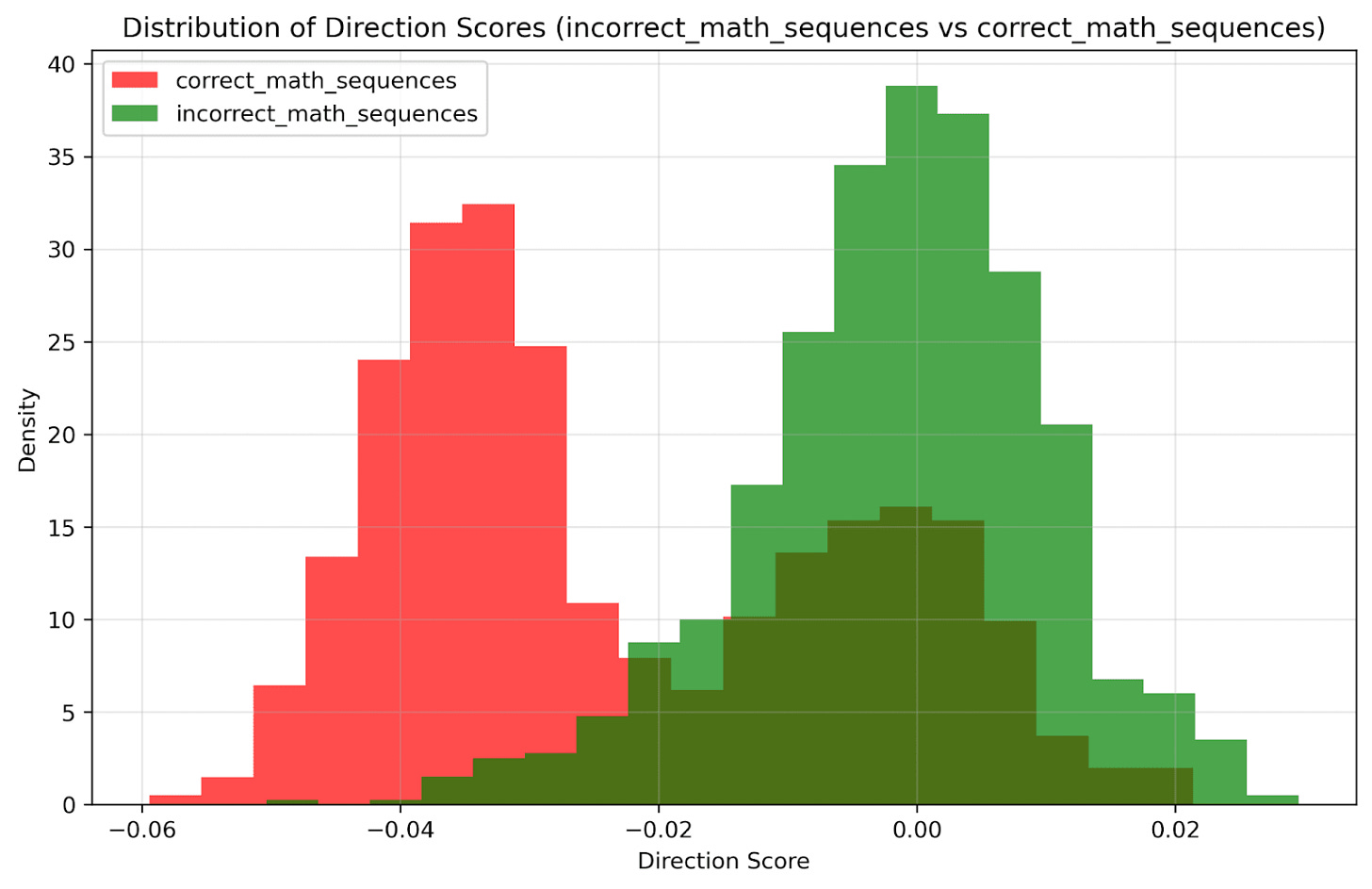
Results:

• Addition: 80% train, 76% test accuracy

• Multiplication: Below chance performance

• Subtraction: Below chance performance

Interpretation: The model shows limited mathematical understanding, primarily for simple addition. This likely reflects training data patterns rather than genuine arithmetic reasoning.

Code Validity: Strongest Signal

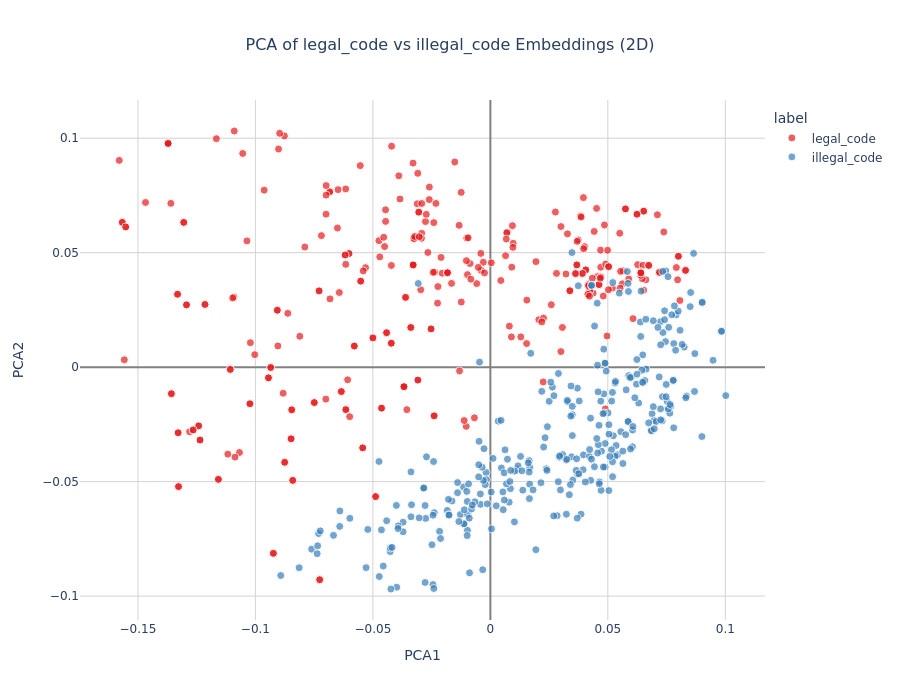
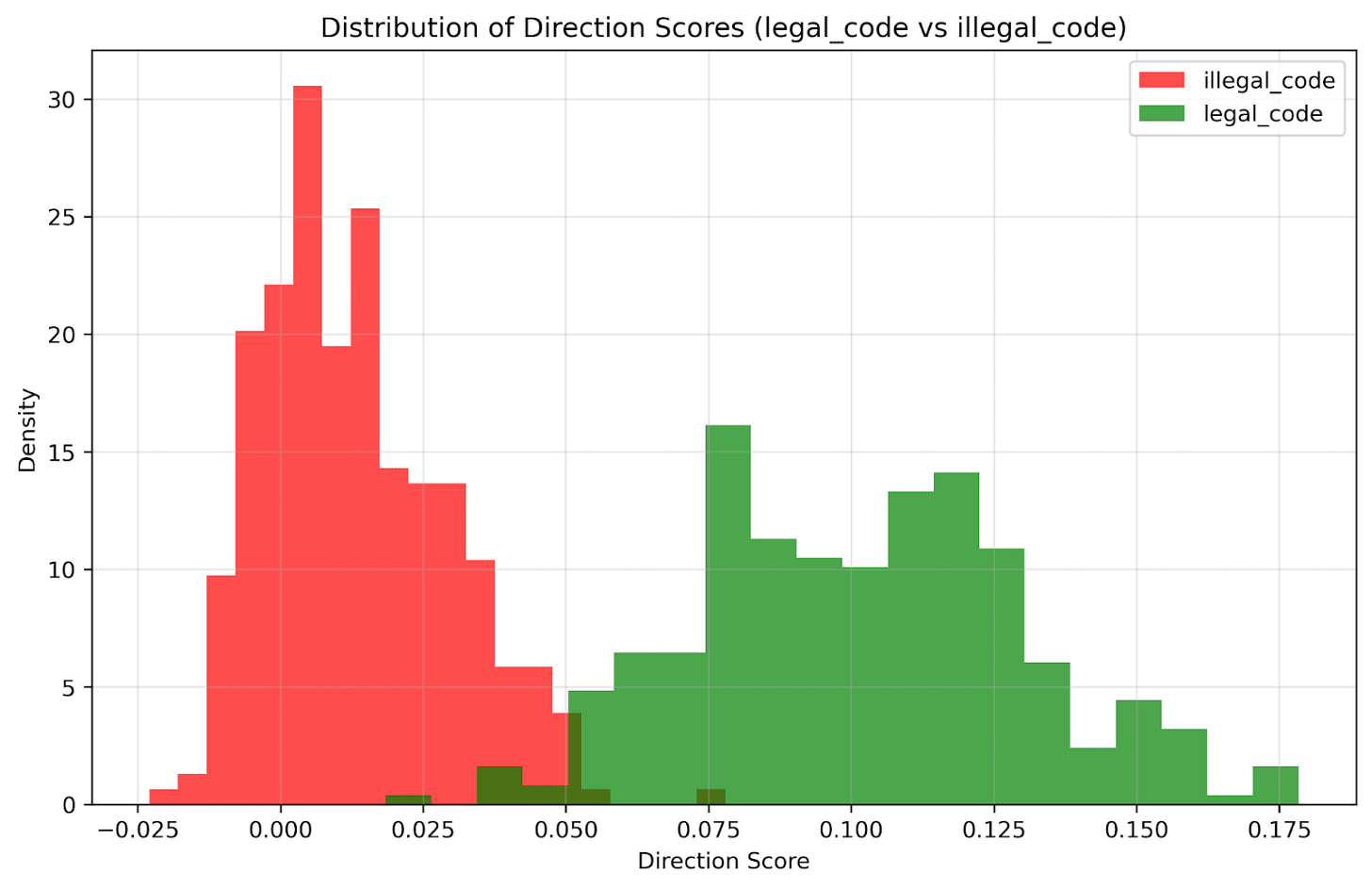
Setup: Tested uniformly named Python functions where some produced valid "Hello World" output while others contained runtime errors (division by zero, syntax errors, etc.).

Figure 5: 2D PCA representation of individual sentence embeddings for code experiment. Each dot represents a Python function, where red is from legal code sequences (i.e. printing a string or adding something to a dictionary), and blue is from invalid code (i.e. trying to divide by zero).

Figure 6: Distribution of Direction Scores for valid vs. invalid code sequences. Scores are derived by projecting SONAR sentence embeddings onto the weight vector of a trained logistic regression probe. The separation of the valid (green) and invalid (red) distributions confirms that the probe successfully identified a linear direction for non-failing/valid code within the model's embedding space.

Results:

• PCA showed clean separation between valid and invalid code

• Logistic regression: 98% train, 96% test accuracy

• Strongest correctness signal we observed

Here we formulated our main hypothesis:

Decoder Efficiency Hypothesis: Valid code patterns may be fundamentally easier to reconstruct than syntactically/semantically broken code. Valid structures follow consistent rules, making them more compressible. The model likely develops shortcuts for common valid patterns.

One can see this as proof of Kolmogorov Complexity in the wild.

Chess: Syntax vs Semantics

Lastly, we wanted to venture into realms of SONAR’s training test corpus that are harder to approximate using N-Grams, to see if our results so far are product of a sophisticated pattern matcher, or something more akin to genuine understanding.

First, we investigated whether we can predict from the internal embeddings whether a playout of a Chess game is legal (according to the rules of Chess itself). Importantly, we did not test whether we can predict whether a random string is in PGN notation, but rather whether a seemingly legal playout in PGN notation is legal. Therefore, this requires understanding of the rules of chess, i.e. knowing that a pawn cannot move three squares.

Also, an important distinction is that these playouts were randomly generated. From all possible playouts of Chess games, only a few are contained in SONAR’s training test corpus. By using randomly generated chess games, we ensure this is not approximatable by an N-Gram approximator.

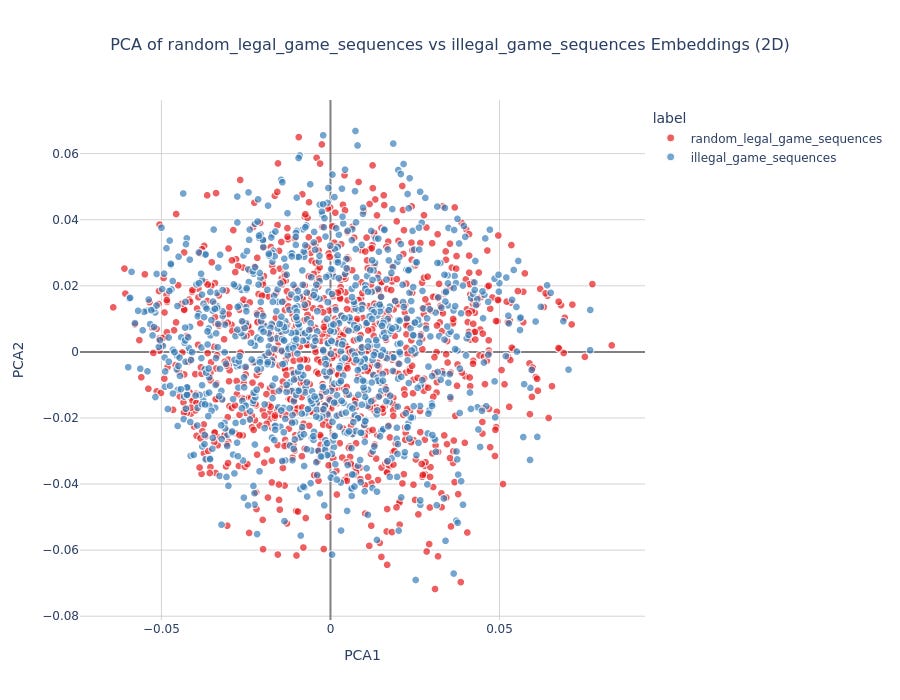
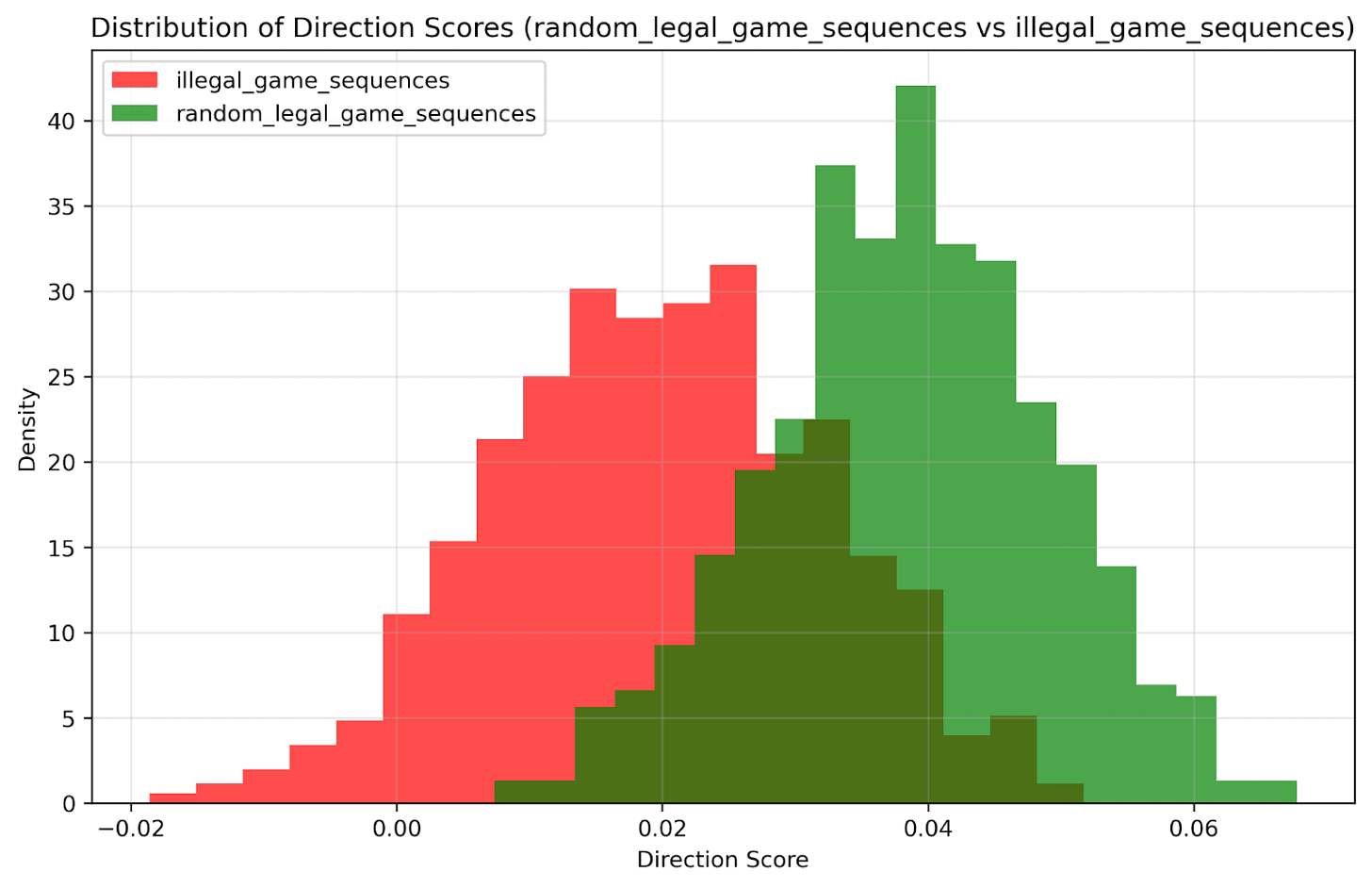
Syntactic Experiment: Generated random chess games in PGN notation, then introduced illegal moves. Tested whether embeddings could distinguish legal from illegal move sequences.

Figure 7: 2D PCA representation of individual sentence embeddings for chess experiment. Each dot represents a Python function, where red is from legal chess PGN sequences, and blue is from illegal chess PGN sequences.

Figure 8: Distribution of Direction Scores for chess experiment. Scores are derived by projecting SONAR sentence embeddings onto the weight vector of a trained logistic regression probe. The weak separation of the valid (green) and invalid (red) distributions confirms that the probe struggles with identifying a linear direction to separate valid vs. invalid PGN chess sequences. More critically, this depends on the number of randomized (and thus illegal) chess moves.

Results:

• No clear PCA separation for legal vs illegal games

• Logistic regression accuracy correlated with number of illegal moves

• More illegal moves → better classification accuracy

• Suggests weak sensitivity to chess syntax, but not robust understanding

To test this further, we checked whether we can probe for board state features directly. This tests whether the model is not just checking the syntax of PGN notation, but is checking the syntax by having an emergent world representation of the board game.

Semantic Experiment: Probed directly for board state features after observing game sequences. Attempted to predict:

• Whether white queen remains on board

• Piece advantage

• Other positional features

Figure 9: Probing for an internal chess board representation in SONAR. The chart compares the accuracy of linear probes (blue) trying to predict board state features against a majority class baseline (red). The probes consistently perform at or below the baseline, suggesting SONAR lacks a semantic understanding of the chess game state.

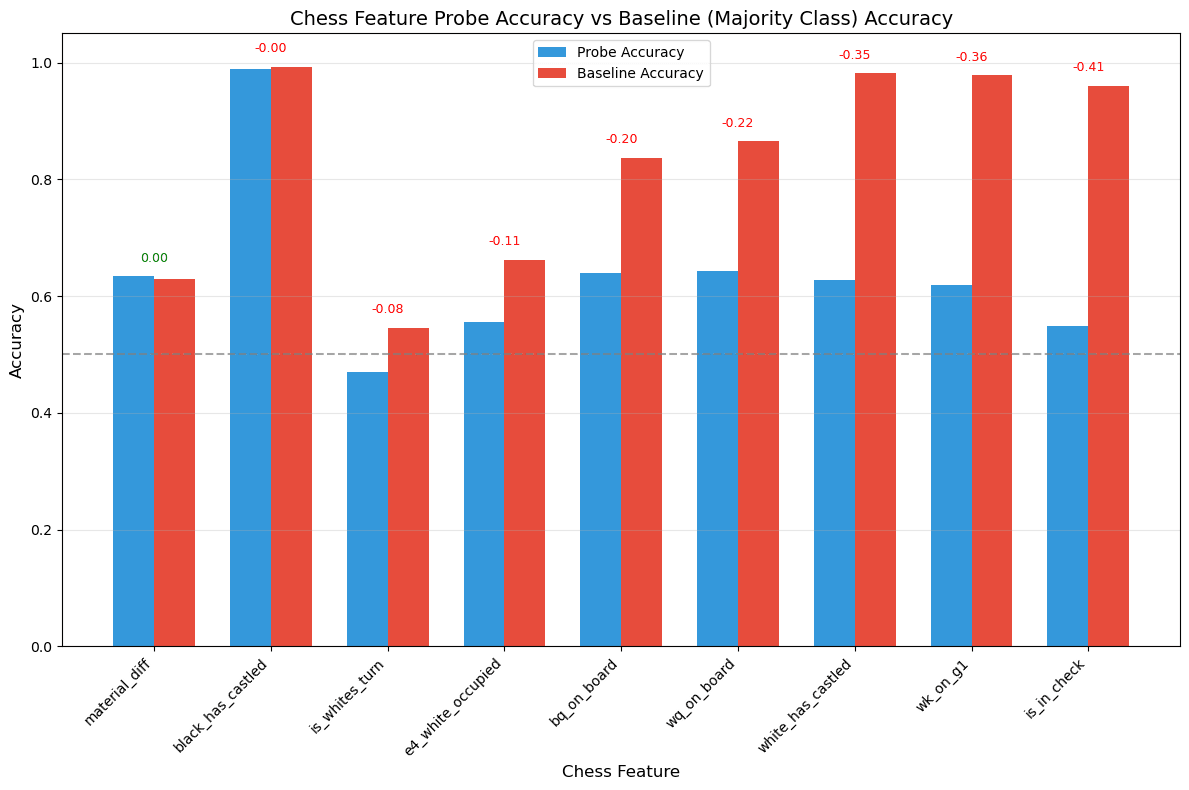
Results:

• Accuracy no better than majority class baseline across all features

• No evidence of internal board state representation

As we can see, SONAR lacks semantic chess understanding. It may recognize some syntactic patterns but doesn't maintain meaningful game state representations.

Discussion

We observe a clear hierarchy of correctness understanding in SONAR:

1. Code validity (strongest): 96% accuracy, clean separation

2. Language grammaticality: 93% accuracy, cross-lingual robustness

3. Basic arithmetic: 76% accuracy, limited to addition

4. Chess legality: Weak, context-dependent signal

5. Chess semantics: Absent above baseline

Emergence from Compression Efficiency

For code and language, our explanation centers on compression efficiency. Valid patterns follow regular structures that are inherently more compressible than random sequences (think Kolmogorov complexity). The autoencoder develops an "agent overhang", i.e. correctness understanding emerges naturally from the reconstruction task rather than explicit training.

Decoders implicitly learn correctness because it improves reconstruction accuracy. If you know something follows grammatical rules or valid code syntax, you have powerful constraints that make decoding easier.

Training Data Dependency

The hierarchy likely reflects training corpus composition:

• Code and natural language: Heavily present in training data

• Basic arithmetic: Less frequent, explaining weaker signals

• Chess notation: Rare, especially random game sequences never seen during training

This suggests the model's correctness understanding is fundamentally tied to pattern frequency rather than abstract reasoning capability.

Limitations

1. With only one week, we limited ourselves to two analysis methods. Absence of evidence isn't evidence of absence. Different probing techniques might reveal hidden chess representations or other correctness signals.

2. Our notion of chess "understanding" may differ from the model's internal representations. A non-linear board state encoding could exist that our linear probes can't detect.

3. We didn't explore other correctness domains like logical reasoning, factual accuracy, or causal relationships.

4. Linear probes can sometimes find spurious patterns. More sophisticated analysis would strengthen these conclusions.

Conclusion

SONAR autoencoders develop varying degrees of internal correctness representations, with strongest signals in code validity and language grammaticality. This pattern suggests correctness information emerges as a byproduct of efficient encoding-decoding rather than explicit training for correctness detection.

Practical Implications:

• Autoencoder representations contain exploitable correctness signals

• Hierarchy reflects compression efficiency rather than reasoning depth

• Cross-lingual grammaticality suggests universal syntactic encoding

• Potential applications in automated correctness detection tasks

Future Directions:

• Non-linear probing methods for chess and other domains

• Investigation of logical reasoning capabilities

• Analysis of factual correctness representations

• Comparison across different autoencoder architectures

The key insight: correctness understanding in language models may be less about sophisticated reasoning and more about the fundamental mathematics of compression. Valid structures are easier to encode, decode, and reconstruct. This makes correctness a natural emergent property of the autoencoding objective.